CFD simulation of drag: advanced calculation to improve aerodynamics
Introduction....
The impact of thermal plumes outside the building is difficult to predict due to the various variables that design engineers and architects are unable to control. These variables include wind speed, air temperature and humidity, wind direction and other activities surrounding the building. However, these phenomena have an impact on the performance of equipment positioned outdoors.
EOLIOS accompanies you in the study of the impact of these problems to ensure an optimal operation in all circumstances, even the most extreme.
Our Data Center projects :
What is drag
Definitions
Drag is a resistive force that opposes the motion of an object as it moves through a fluid, such asair orwater.
It is generated by theinteraction between the object and the fluid, and manifests itself in the form of fluid friction and pressure forces.
Drag is generally expressed in Newtons (N) and is often quantified using a quantity called the drag coefficient.
Theuse of the drag coefficient goes back centuries, with the first observations and efforts to understand drag forces in an aerodynamic context.
However, it was in the 19th century that scientists such as George Gabriel Stokes began to formalize the concept and develop mathematical theories to quantify drag. Since then, research and progress on drag have played a key role in the development of fields such asaviation,automotive, building design and various sports-related activities.
In a nutshell, drag is a resistive force encountered when moving an object through a fluid.
The drag coefficient quantifies this resistance.
Understanding and controlling drag is therefore essential for optimizing the performance,efficiency and safety of certain objects in motion or placed in a fluid flow.
The importance of drag coefficient
The drag coefficient is a measurement that quantifies the resistance of air or fluid to the movement of an object. It plays a key role in many fields, such asaviation,automobiles, sliding sports and evenbuilding architecture. Understanding and mastering this force of resistance is crucial to optimizing the performance andefficiency of many applications.
Inaviation, for example, reducing drag is a major concern.
By minimizing drag, engineers can increase aircraft speed andfuel efficiency, reduce fuel consumption and improve range.
Advances have also been made inimprovingaircraftlift, which will be detailed later in this article.
This has led to significant advances in aircraft wing design, for example.
Theautomotive industry is also looking to minimize this drag to reduce fuel consumption and improve range.
This issue is all the moretopical with theemergence of electric vehicles.
Motor sports (such as Formula 1), on the other hand, seek to maximize aerodynamics to improve the handling, stability and performance of racing cars.
Similarly, in sliding sports such as downhill skiing, snowboarding or even cycling, drag reduction enableshigher speeds to be reached by minimizing drag forces and optimizing air penetration.
This is leading to advances in the design of cycling helmets, for example, as well as other sports equipment, to minimize drag and maximize the athlete’s performance.
Building architecture is also influenced by the principles of drag.
By designing aerodynamic structures, architects can reduce the forces exerted by strong winds, thereby improving the safety and stability of structures such as bridges.
The drag coefficient is therefore a crucial measurement in many areas involving interaction betweenan object and a fluid. Understanding and controlling these drag forces is essential for optimizing the performance,efficiency and safety of many aerodynamic applications.
Calculating the drag coefficient
Definition
The drag force is given by the following formula: D = ½ρCxSv²
In which :
- ρ is the density of the fluid,
- v is the relative velocity between the object under study and the fluid,
- S is the object’s reference surface, i.e. the projection of the object onto a plane perpendicular to the main direction of flow,
- Cx is the drag coefficient (sometimes also referred to as C_D).
This force therefore depends on the characteristics of the fluid (density), theobject ( shape and roughness) and the relative velocity between the object and the fluid.
The drag coefficient Cx is a quantity that accurately quantifies the aerodynamic resistance of an object in a moving fluid.
It is obtained by relating the drag force experienced by the object to the dynamic pressure and the corresponding reference surface: Cx = 2D/ρSv².
Note that the drag coefficient is not a constant quantity: it depends on the properties of the flowing fluid, the shape of the object and the roughness of the surface.
Further on, we show that the C_D coefficient depends on the Reynolds number.
Note: The lift coefficient (orbearing coefficient in some cases) is defined in the same way: F_L = ½ ρ C_L S v²
In this formula :
- ρ is the density of the fluid,
- v is the relative velocity between the object under study and the fluid,
- S is the object’s reference surface, i.e. the projection of the object onto a plane perpendicular to the main direction of flow,
- C_L is the lift coefficient(L for Lift ).
In some cases, this is referred to as lift(F_L > 0) or downforce(F_L < 0).
Drag coefficient and Reynolds number
The Reynolds number (Re) is a dimensionless quantity that characterizes the flow regime of a fluid.
It is calculated by dividing the product of the fluid’s velocity, characteristic length (such as the diameter of a cylinder) and density, by its kinematic viscosity:
Re = ρvL/μ
Where:
- v is the fluid velocity,
- L is the characteristic length,
- ρ is the density of the fluid,
- μ is the kinematic viscosity of the fluid.
The Reynolds number determines whether the flow is laminar(low Re) or turbulent(high Re).
Laminar flow corresponds to a low Reynolds number, meaning that fluid particles move in regular, ordered layers around the object.
Conversely, turbulent flow is characterized by a high Reynolds number, where fluid particles move in a chaotic, irregular fashion.
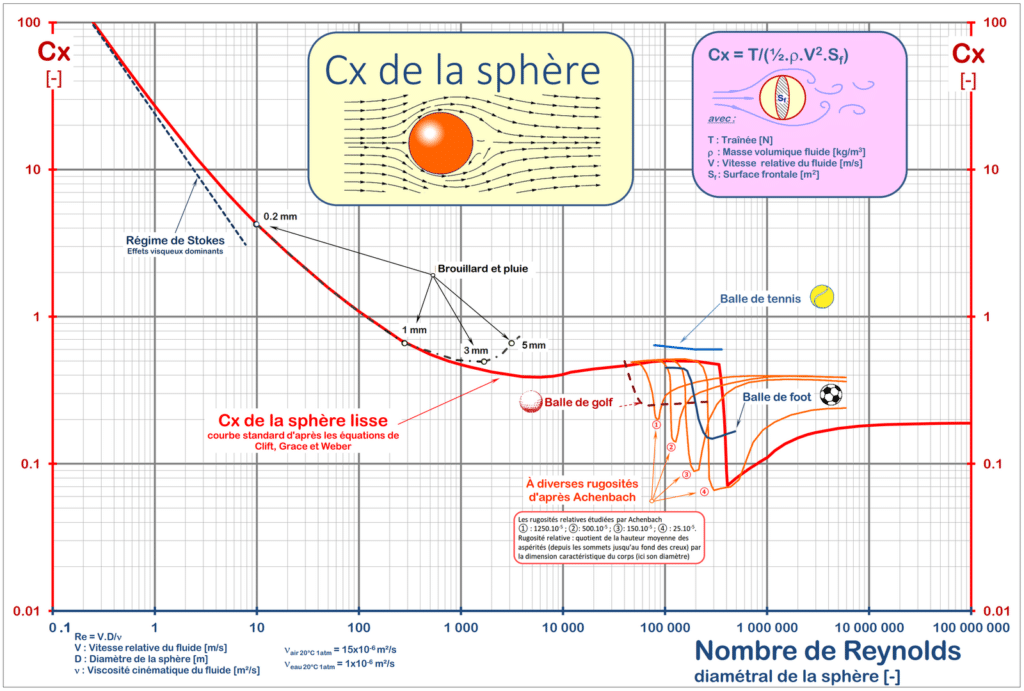
We show that the drag coefficient depends on the Reynolds number.
Let’s take the example of an object with a simple geometry.
If we take the example of a smooth sphere (red curve in the figure below), we initially notice that the drag coefficient(Cx) decreases as the Reynolds number increases, then stabilizes at around a constant value.
There’s a narrower range at higher Reynolds numbers, where the Cx falls, then rises again to reach a more or less constant value.
This phenomenon is known as a drag crisis and marks the transition from laminar flow to turbulence.
More precisely, it is linked to a later take-off of the boundary layer on the surface of the object.
Let’s take the golf ball as an example: the dimples on the ball’s surface promote the transition to turbulence and allow the boundary layer to re-bond.
With a Reynolds between 10⁴ and 10⁵, this places the golf ball in the drag crisis domain, as indicated by the curve, and therefore allows the ball to travel greater distances.
Influence of body shape on drag
The shape of a body has a major influence on the drag force exerted on it.
Objects with a streamlined or aerodynamic shape, such as aircraft or racing cars, generally have lower drag coefficients.
This is due to the reduction in the surface area interacting with the air, and the creation of smoother, more laminar airflows over the object’s surface.
On the other hand, objects with a flatter or more angular shape, such as most trucks or buildings, generally have higher drag coefficients.
These shapes create more turbulence and vortices in the air, increasing resistance to flow and drag.
Vehicle aerodynamics
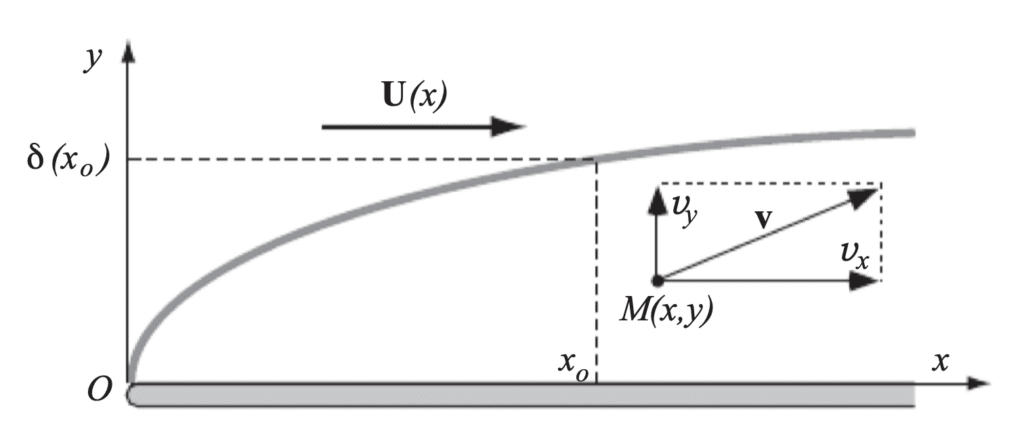
Notion of boundary layer
The boundary layer is a thin region near the surface of an object where the effects of fluid viscosity become significant.
In other words, it’s a zone where fluid velocity near the object’s surface is slowed down by friction with that surface.
It plays a crucial role in many fluidic phenomena, including the transition between laminar and turbulent flow, and the formation of wakes behind moving objects.
The concept of the boundary layer, developed by Ludwig Prandtl in 1905, needs to be adjusted to suit different practical situations, particularly in the presence ofturbulent flows upstream of a body or in the boundary layer.
These conditions lead to significant changes in flow velocity profiles, with the appearance of a turbulent boundary layer.
What’s more, when solid bodies are poorly profiled, this can lead to boundary layer lift-off, generating a turbulent wake downstream of the body.
In these scenarios, theresulting flow no longer behaves like a perfect fluid, leading to a significant increase in energy dissipation and drag force on the body.
Aircraft wing - Boundary layer control
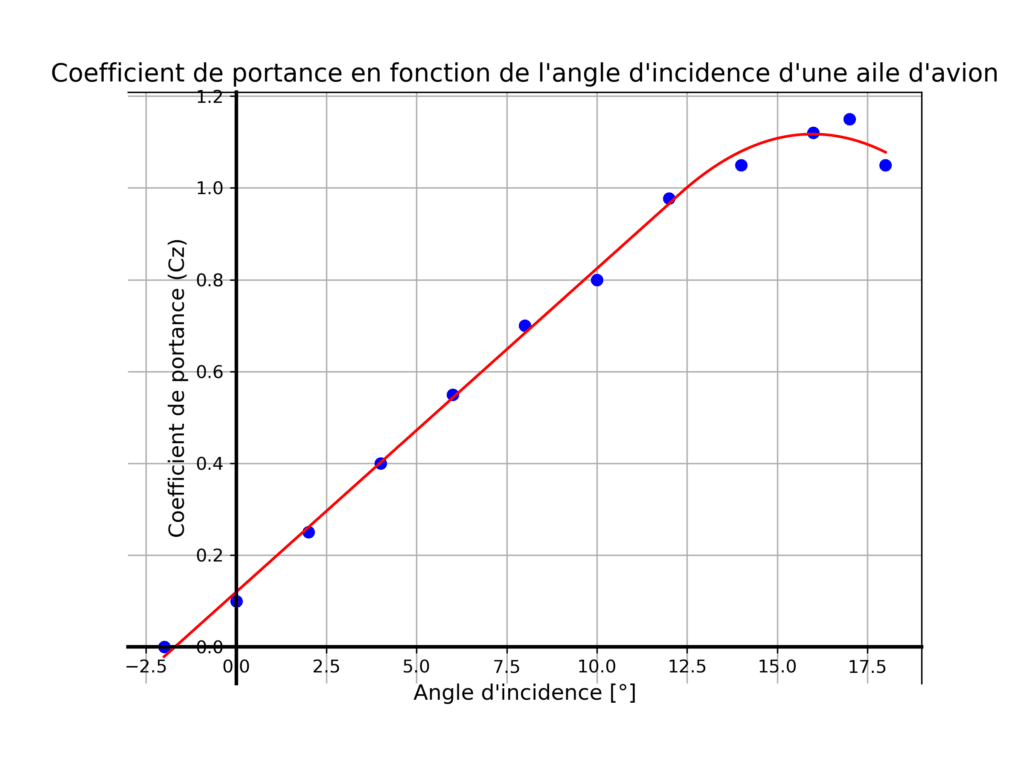
The most important aerodynamic force for an aircraft wing is the lift force.
This force is generated by the Magnus effect, thanks to the circulation of speed around the wing.
To keep the aircraft in flight, the lift force(F_L or L for Lift ) must compensate for its weight.
This force increases proportionally to the square of the velocity(v), and increases linearly with theangle of incidence(α) when the latter is low.
We show that for an aircraft wing, the lift force is of the order of :
F_L ∼ ρ b l v² sinα
Where:
- ρ is the density of the fluid,
- b is thewing span,
- l is the wing chord,
- v is the airspeed of the wing (i.e. the speed of the aircraft),
- α is theangle of incidence.
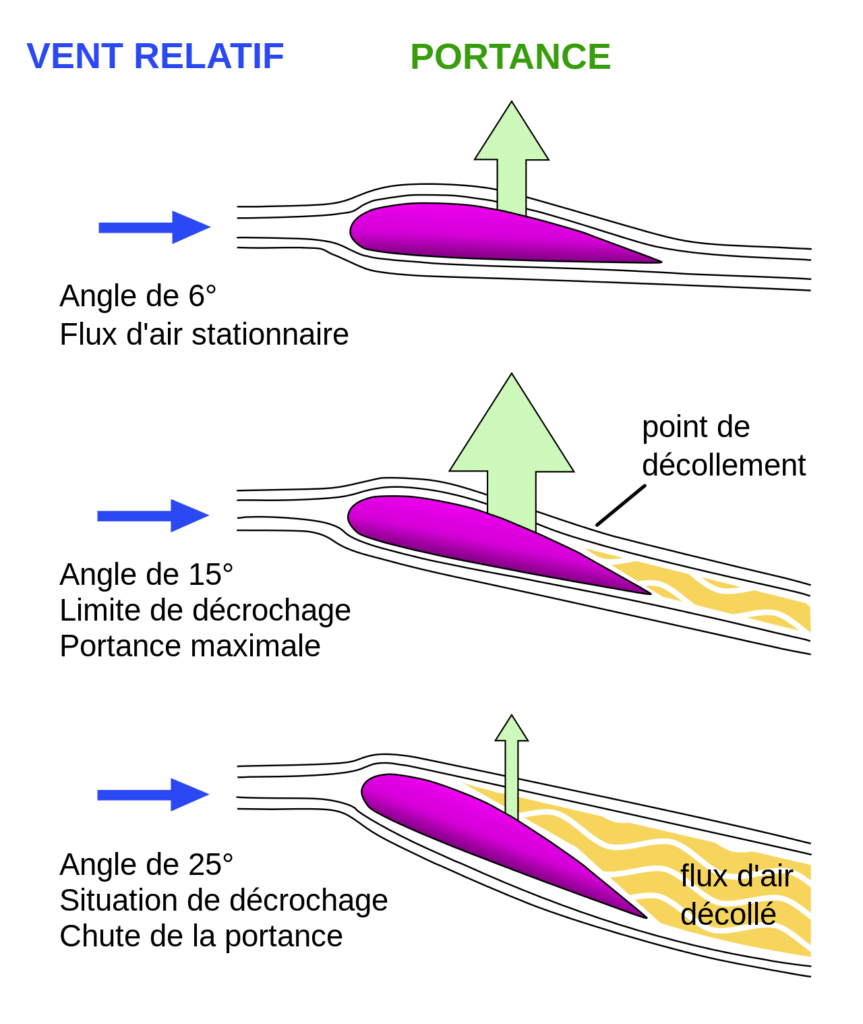
Note that as theangle α increases, so does the lift.
This is thedesired effect on a wing.
However, when α increases too much and reaches a critical value α_c, the stall phenomenon occurs: lift decreases sharply and the above formula is no longer valid.
It should therefore be avoided, especially incivil aviation.
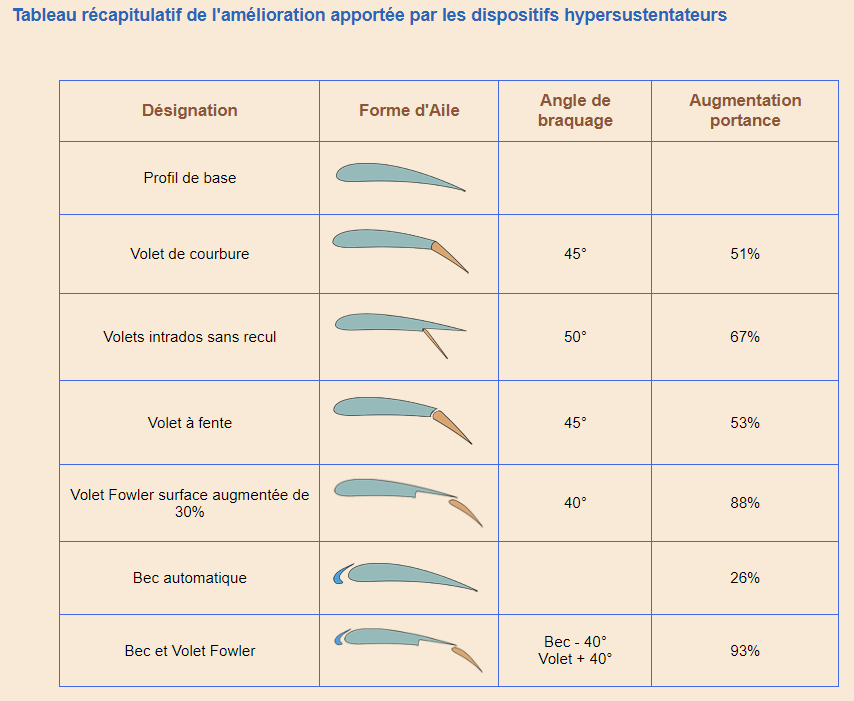
Two common approaches to improving wing performance are: increasing the critical angle of incidence by using slats on the leading edge, and increasing the lift coefficient for a given angle of incidence by using trailing edge flaps.
-
Leading edge slats increase thecritical angle of incidence by reactivating theupper surface boundary layer through theinjection of tangential air from thelower surface, thus reducing the effect of the inverse pressure gradient at high incidence.
- Trailing-edge flaps increase airflow around the airfoil, resulting in higher lift at a given angle of incidence.
On large aircraft, these flaps can be used in series to increase lift on take-off andlanding.
They reactivate the upper surface boundary layer and induce a strong downward deviation of the flow velocity, which increases lift and circulation.
Land vehicles
Issues
In the context of land vehicles, minimizing drag is a crucial objective for improvingfuel efficiency.
This drag force is mainly generated by the pressure difference betweenthe front and rear of the vehicle as it moves through the air.
Unlike aircraft, where friction with the air is the main contributor to drag, in the case of land vehicles such as cars, pressure plays a predominant role.
CFD simulation of the thermo-aerodynamic effects of an industrial plant in an urban area
An important characteristic of cars is that the force of lift must be directed downwards to maintain good grip of the tires on the road.
This contributes to better handling, but it’s also crucial not to have excessive lift, as this can lead to premature tire wear and excessive friction. So finding the right balance between reducing drag and maintaining sufficient lift to ensure vehicle safety and stability is a challenge for automotive engineers.
Drag reduction
Efforts to reduce drag focus in particular on designing more aerodynamic body shapes.
Over the years, automakers have succeeded in reducing the coefficient of drag(C_x or C_D) from over 0.5 for older cars to less than 0.3 for modern vehicles.
This reduction in C_D helps improve vehiclefuel efficiency by reducing air resistance, which translates into lower fuel consumption.
However, drag reduction must be balanced with other design requirements, such asvehicle habitability.
For example, certain body shapes that could further reduce drag could compromiseinterior space or visibility for drivers, necessitating design compromises.
A large proportion of drag is generated at therear of the vehicle, where complex phenomena such as boundary layer lift-off and vortex formation influence air resistance.
Engineers use standard models such as Ahmed’s body to model these phenomena and study the impact of different design parameters, such as theangle of the rear window, on drag.
Studies of vehicle aerodynamics reveal that drag varies non-monotonically with theangle of inclination.
For example, at low angles, the contribution of transverse recirculation can be reduced, while the effect of axial vortices is amplified.
This underlines the complexity of vehicle aerodynamics and the need to consider a multitude of factors in the design to optimize overall performance.
Finally, it’s crucial to maintain sufficient negative lift to ensure good roadholding, especially at high speeds.
This ensures sufficient tire pressure on the road for optimum grip.
As a result, carmakers have to strike a delicate balance between reducing drag and maintaining vehicle stability and safety at different speeds and driving conditions.
For racing vehicles such as Formula 1 cars, which travel at speeds of around 250 km/h, systems such as ailerons are used to improveaerodynamic downforce.
It should be noted, however, that these systems increase drag.
Active or passive control of drag or lift
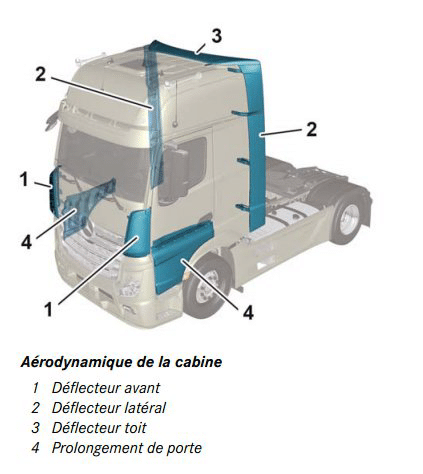
Aerodynamic improvements, such asadding roof deflectors to trucks or modifying the shape of rear-view mirrors, can reduce drag passively, without energy input.
In active control, the action is adjusted in real time according to flow conditions, either manually by the pilot in open loop, or automatically by a computer in closed loop.
For example, to prevent boundary layer delamination, air can be sucked in or injected close to the wall to maintain a stable flow, although this requires additional power and is little used in practice.
Closed-loop reactive control, still in the research phase, involves devices such as motorized vortex generators to reduce drag, demonstrating potential applications in various fields, particularly aeronautics.
Calculating drag coefficients in CFD simulations
Benefits of CFD simulation
The use of computational fluid dynamics (CFD) offers several advantages over traditional wind tunnel testing.
Firstly, CFD enables virtual simulations to be carried out, avoiding the costs and delays associated with building and operating physical wind tunnels.
Wind tunnel testing requires specialized facilities, with expensive models and precise measurement equipment.
CFD, on the other hand, is performed on computers, considerably reducing costs and time.
Secondly, CFD allows greater flexibility in design and study parameters.
It is easier to modify object geometry, flow conditions or fluid properties in a CFD simulation than in a real wind tunnel.
This allows a greater number of scenarios to be realized and different configurations to be explored, resulting in more efficientdesign optimization.
In addition, CFD offers better visualization and more detailed analysis of results.
Numerical simulation enables flow lines, turbulence zones, pressure gradients, etc. to be visualized, providing detailed information on the flow in and around the object under study.
This enables us to better understand aerodynamic phenomena andidentify potential areas for improvement.
Finally, CFD enables us toexplore a wider range of flow conditions.
Whereas wind tunnel testing is limited by equipment capabilities and ambient air conditions, CFD can simulate extreme conditions, high speeds, different temperatures and so on.
This offers greater flexibility for testing and validating object performance in real-life conditions, which Eolios is able to achieve.
Determining aerodynamic coefficients
To determine the drag coefficient (and lift coefficient), whether using CFD simulation or experimental methods, we need to understand the pressure distribution over the body surface.
Viscous shear forces must also be taken into accountover the entire surface of the object under study.
This helps optimize performance in terms of lift, drag and stability.
By integrating the pressure distribution over the object’s surface, we can derive the object’s drag force and drag coefficient.
Thanks to the use of CFD software, the value of aerodynamic coefficients can be predicted directly after simulation.
Determining aerodynamic coefficients is a crucial step in the design andoptimization of any object subject to aerodynamic forces.
This information helps toimprove performance in terms of drag, lift and stability, and is essential in many fields such asaeronautics,automobiles and sports.
Formula 1 CFD simulation
context
Aerodynamics play a crucial role in the performance of Formula 1 cars, where every millisecond counts in competition.
An aerodynamically well-designed car can generate high levels of downforce, improving tiregrip and enabling higher cornering speeds.
In addition, reduced aerodynamic drag enables the car to reach higher top speeds on the straights, improving overall performance.
In this context, CFD simulation has become an indispensable tool for Formula 1 teams.
CFD enables engineers to numerically model the behavior of airflow around the car, taking into account parameters such as velocity, pressure and turbulence.
This precise, detailed modeling provides crucial information on how different aerodynamic configurations affect the car’s performance.
In particular, the simulation provides precise values for aerodynamic coefficients and forces acting on the car.
In this context, Eolios has carried out simulations on a Formula 1 car to determine the values of these aerodynamic coefficients and highlight the phenomena responsible for the various forces applied to the car.
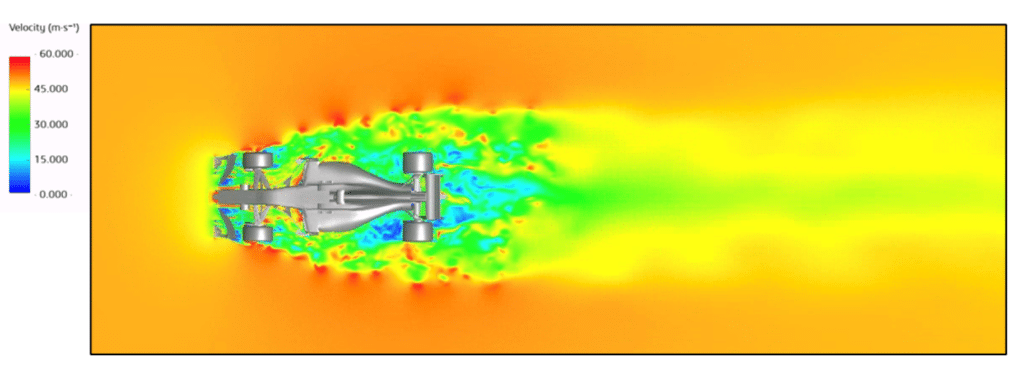
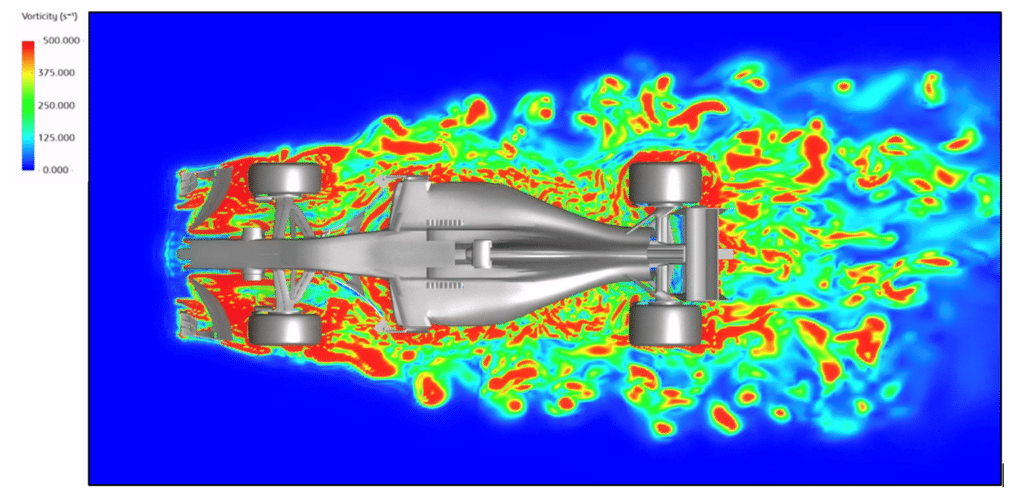
Speed field
In the figures above, themain observation is that the presence of the car significantly disturbs the surrounding velocity field.
This disturbance is particularly noticeable at therear of the car, where the velocity field is described as“highly disturbed and disordered“, typical of turbulent flow.
Turbulent flow is characterized by its irregularity and complexity, resulting from the formation of vortices, pressure fluctuations and chaotic movements of fluid particles.
In the context of moving vehicles, turbulent flow can be generated by boundary layer separation around the body, flow waves due to vehicle contours, as well as interactions with the surrounding air.
These turbulent flow characteristics can have a variety of implications, including increased aerodynamic drag, reduced fuel efficiency and increased vehicle instability at high speeds.
Understanding and modeling turbulent flow is therefore essential to optimize vehicle design and improve performance in terms of aerodynamics, fuel efficiency and stability.
Drag force
In the following figures, we display the pressure planes to show the effect it has on the car, in other words to highlight the drag force on the Formula 1.
Behind the car, you’ll notice an area of depression which is largely responsible for the drag.
Behind the formula, thevortex flow is detrimental to aerodynamics, and is due to the fact that the air has difficulty in bypassing the object.
This difficulty creates an overpressure before the car, then a depression after the plate.
In F1 racing, drivers take advantage of the low pressure at the rear of the car in front to overtake: the overtaking car no longer has to ” split ” the air like the car in front, and the pressure difference between front and rear, and therefore drag, is reduced.
We say that the car takes advantage of the ” suction ” to overtake.
CFD simulation software is used to determine the values of the forces acting on the car and the values of the aerodynamic coefficients.
In the simulations we have carried out, the drag coefficient is evaluated at around 0.92, which is the standard value for a Formula 1 car.
The value of the drag force is: F = 1900N.
By performing the theoretical calculation using the following formula:
F = ½ ρ Cx S v²
And taking a surface area S = 1.5 m², we find Fd = 2070 N, which is close to the value calculated by the software during simulation, bearing in mind that the surface area S used to calculate this theoretical order of magnitude is not exact but approximate.
Vorticity
Vorticity measures the rotation of a fluid around a local axis.
When an object, such as a car, passes through a fluid such as air or water, it disturbs its flow.
This creates vortices, where the speed and direction of the fluid change.
These vortices generate vorticity, indicating theintensity and location of the rotations.
In the context of the plans shown, which display vorticity, we can visually observe how the presence of the car influences the fluid flow around it.
Areas of high vorticity generally correspond to those where vortices are most intense, often downstream and to the sides of the car.
Thevisual analysis we have carried out using these simulations provides a better understanding of theinteraction between the moving car and the surrounding fluid, which is crucial in many areas such as Formula 1aerodynamics.
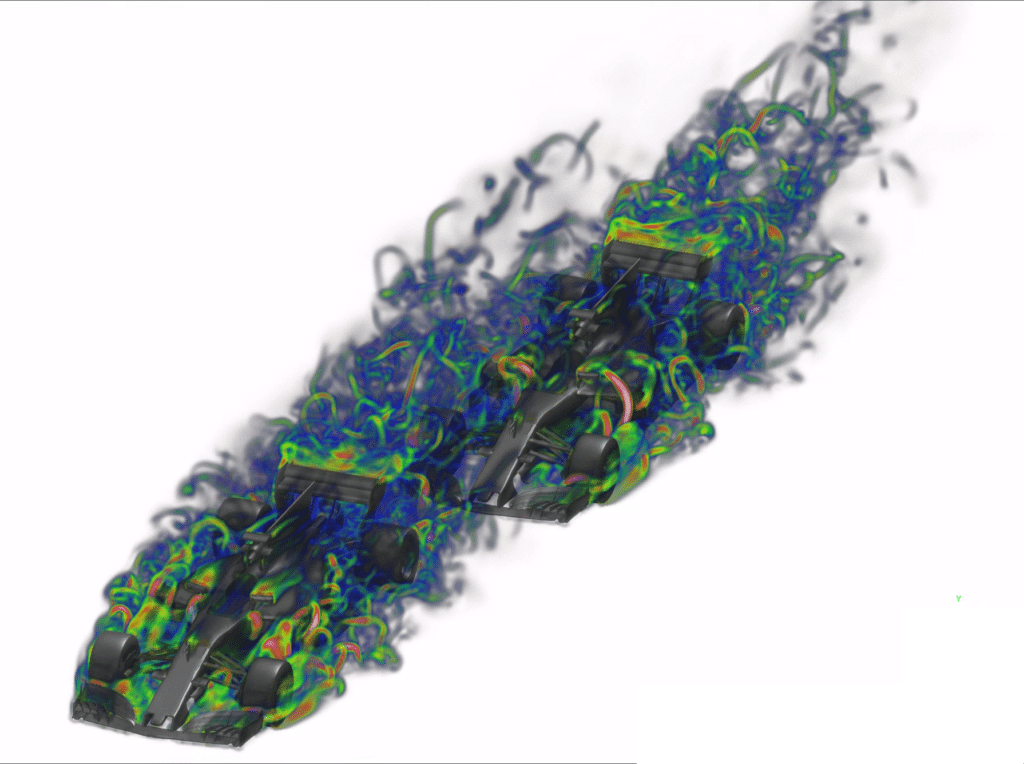
Suction effect: simulation of a Formula 1 car in overtaking phase
Another simulation aims to estimate the drag force of a racing car when it is sucked in by the vehicle in front of it, just before overtaking it.
The configuration examined is shown in the image below.
When one Formula 1 car overtakes another, the aerodynamic forces acting on each car are greatly influenced by their relative positions.
The overtaking car benefits from a significant reduction in air resistance, as it benefits from thesuction effect generated by the car it is trying to overtake.
This reduction in resistance, often measured by a reduction in the drag coefficient, enables the car to gain speed, whilerequiring less power to maintain acceleration.
In addition, the overtaken car suffers an increase in drag coefficient due to the disruption of airflow caused by the proximity of the car behind it.
These phenomena show just how closely race dynamics are linked to aerodynamic interactions between vehicles, and underline thecrucial importance of drag positioning and management in the overall Formula 1 overtaking strategy.
Balance sheet
Aerodynamic forces, particularly drag, play a crucial role in many fields, fromaeronautics andautomobiles to sports and buildings.
Understanding and minimizing these forces can improve theefficiency, safety and durability of vehicles and structures.
Computational Fluid Dynamics ( CFD) simulation is emerging as an essential tool, offering a far more accessible and cost-effective approach than wind tunnel testing.
It enables detailed analysis of aerodynamic phenomena, paving the way for more efficient designs and faster innovation in a variety of sectors.
